پاسخ چالش اول

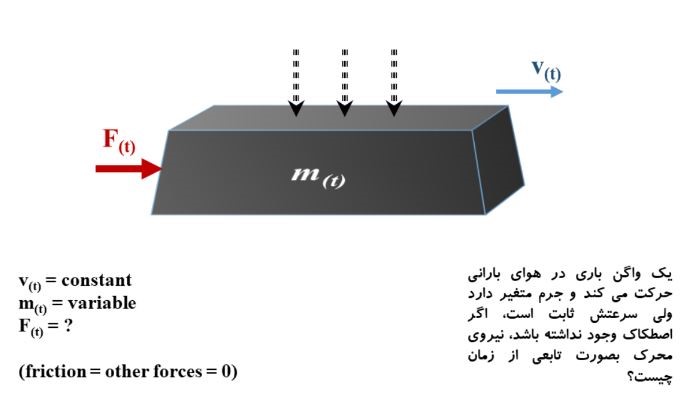
پاسخ من به این سؤال بر اساس دانستههای شخصی من از فیزیک:
درصورتی که با سرعت ثابت خطی، جرم افزایش پیدا کند مطابق فرمول انرژی مکانیکی جنبشی خطی
\[E_{k{(t)}}=\frac12m_{(t)}v_{(t)}^2\]
\[v_{(t)}= |\vec{v}_{(t)}| \]
انرژی جنبشی جسم افزایش پیدا میکند درنتیجه به سیستم انرژی وارد شده است(یعنی نیرویی روی سیستم کار انجام داده است).
از طرفی بر اساس فرمول کار داریم:
\[ \mathrm{d}W=\vec{F}\cdot \mathrm{d}\vec{r}\]
و از آنجایی که حرکت خطی است و نیرو و جابجایی هم راستا هستند داریم:
\begin{align} \mathrm{d}E_k=\mathrm{d}W={F} \, \mathrm{d}{x} \tag 1 \end{align}
میدانیم:
\begin{align} v_{(t)}=v_c=\mathrm{const.} \Longrightarrow \left\{\begin{array}{rl} \mathrm{d}x & = v_c \, \mathrm{d}t \\ \\ \mathrm{d}E_k & = \frac12 v_c^2 \, \mathrm{d}m \end{array} \right. \tag 2 \end{align}
در نتیجه:
\begin{align} (1),(2) \Longrightarrow \frac12 v_c^2 \, \mathrm{d}m = {F} \, v_c \, \mathrm{d}t \Longrightarrow F_{(t)}=\frac12 v_c \frac{\mathrm{d}m}{\mathrm{d}t} \end{align}
بنابراین:
\begin{align} F_{(t)}=\frac12 v_c m'_{(t)} \end{align}
....
.
.
.